Caleidoscopio #
«En la memoria del hombre, ninguna invención y ningún trabajo, ya sea dirigido a la imaginación o al entendimiento, jamás producirá un efecto como tal» (Comentario de Peter Mark Roget sobre el caleidoscopio).
El caleidoscopio fue inventado en 1816 por el físico David Browster. Consta de un tubo en cuyo interior hay tres espejos que forman un prisma con las caras interiores reflectantes y en cuyo extremo, encerrados entre dos láminas translúcidas, hay varios objetos de diferente color y forma que se ven multiplicados al girar el tubo.
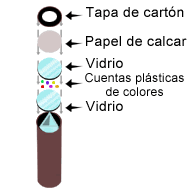Figura 1: Esquema de un calidoscopio hecho artesanalmente.El efecto de un caleidoscopio puede parecer complejo, sin embargo es de sencilla implementación; la escena a continuación es prueba de ello. Los diversos objetos que conforman la imagen se verán reflejados tantas veces como la barra de configuración lo permita
Código del Fragment Shader del efecto: #
caleido.frag
precision mediump float;
uniform sampler2D texture;
uniform float segments;
varying vec2 texcoords2;
void main() {
vec2 coord = 2.0 * texcoords2 - 1.0;
float r = length(coord);
float theta = atan(coord.y, abs(coord.x));
theta *= segments;
coord = vec2(r * cos(theta), r * sin(theta));
coord = (coord + 1.0) / 2.0;
gl_FragColor = texture2D(texture, coord);
}
Como primer paso fundamental, se ejecuta un remapeo de las coordenadas de textura, considerando que lo que se desea es obtener reflejos usando radios como eje de simetría.
vec2 coord = 2.0 * texcoords2 - 1.0;
Ahora el punto \((0,0) \) se convirtió en el centro de la textura y el punto \( (-1, -1) \) es alcanzable en consecuencia. Esto hace posible el manejo de operaciones de rotación.
La rotación es una operación mucho más sencilla de ejecutar en coordenadas polares, de modo que sería ideal transformar la actual coordenada \( (x, y) \) en \( (r, \theta) \)
\[r = ||(x, y)|| \\ \theta = \tan^{-1}\frac{y}{|x|}\]En este nuevo sistema de coordenadas, para rotar basta con modificar el ángulo, es decir, el punto se transforma a \( (r, k\cdot \theta) \) después de la operación, siendo \( k \) el parámetro que indica cuantose desplaza angularmente el punto.
Como el sistema lo requiere, es necesario volver a las coordenadas cartesianas, recordando que \[x = r\cdot \cos(\theta) \\ y = r \cdot \sin(\theta)\]
float r = length(coord);
float theta = atan(coord.y, abs(coord.x));
theta *= segments;
coord = vec2(r * cos(theta), r * sin(theta));
Nótese que los puntos rotarán tanto como segmentos tenga la imagen caleidoscópica deseada.
Finalmente, se regresa al rango usual de coordenadas, \( [0, 1] \) , y el fragmento actual adquiere el color del pixel encontrado en las coordenadas correspondientes.
coord = (coord + 1.0) / 2.0;
gl_FragColor = texture2D(texture, coord);